
Predicting financial outcomes is complex. Monte Carlo simulations offer a dynamic approach by using historical data to estimate expected returns and volatility. Instead of projecting a single outcome, they model a wide range of potential future scenarios by introducing random variables and running thousands of simulations. A key advantage of Monte Carlo simulations is their ability to estimate the probability distribution of complex systems, like investment portfolios with multiple assets, which are difficult to predict due to random variables. By simulating many scenarios, Monte Carlo simulations provide investors with a deeper understanding of potential risks and rewards, enabling more informed decision-making in an ever-changing financial landscape.
The Fundamentals of Monte Carlo Simulations
A Monte Carlo simulation models the probability of different outcomes in processes influenced by random variables, making it a crucial technique for understanding the impact of risk and uncertainty. Named after Monaco's famous gambling destination, where chance and randomness are paramount, this method was initially developed by mathematician Stanislaw Ulam during the Manhattan Project.
Monte Carlo simulations have broad applications in various fields, including finance, where they are used to help investors navigate the unpredictable nature of markets. These simulations are particularly valuable for:
- Risk Management: Assessing potential losses in portfolios or financial positions.
- Value at Risk (VaR) Calculations: Estimating the likelihood of large losses within a portfolio.
- Portfolio Optimization: Determining optimal asset allocation strategies.
- Interest Rate Modeling: Simulating future interest rate scenarios.
- Option Pricing: Valuing complex options where closed-form solutions are not available.
- Project Evaluation: Assessing the viability of investment projects.
At PortfolioMetrics, we use the Monte Carlo method specifically for Risk Management and calculating Value at Risk (VaR), helping investors better understand potential losses. For Portfolio Optimization, however, we leverage the more efficient and faster Mean-Variance model, as seen in our Efficient Frontier tool.
A common analogy to understand the Monte Carlo method is a novice gambler rolling dice. The gambler doesn’t know the odds of rolling a specific number until they throw the dice many times. Similarly, asset prices and portfolio values can seem random, and relying solely on historical data is akin to basing predictions on a single roll of the dice. Monte Carlo simulations consider a broad range of possibilities, reducing uncertainty and providing a clearer picture of potential outcomes.
For instance, in retirement planning, Monte Carlo simulations allow retirees and financial planners to model various scenarios, such as different withdrawal rates or market downturns. The simulation runs thousands of scenarios, each with different variables, to provide a distribution of potential outcomes. This gives retirees insight into the likelihood of various scenarios, from worst-case to best-case, helping them make informed decisions about their financial future.
The Process of calculating the Monte Carlo Simulation
Monte Carlo simulations revolve around the idea that random variables can influence the prediction of outcomes. They focus on repeatedly running simulations with random samples to generate a range of possible future scenarios. Here's a simplified process for simulating portfolio returns using the Monte Carlo method:
- Estimate Model Parameters: Start by calculating the average daily returns for each asset in the portfolio. Additionally, determine the covariance between the assets, which represents how their returns move relative to each other.
- Generate Random Returns: For the forecast period, generate random daily returns for each asset. These returns are drawn from a normal distribution based on the historical average return and volatility of each asset.
- Correlate the Returns: Correlate the random daily returns of individual assets according to their covariance. This ensures that assets with historical relationships (positive or negative correlation) continue to behave similarly in the simulation.
- Weight the Returns: Apply the portfolio's asset allocation to the correlated returns. Each asset's return is weighted according to its share in the portfolio, producing the total return for the portfolio for each simulation.
- Run Multiple Simulations: Repeat steps 2 through 4 thousands of times to generate a wide distribution of portfolio returns. This will provide insights into the range of possible outcomes and the likelihood of different returns.
Example of the use of Monte Carlo Simulations in an investment strategy
Consider an investor contemplating the purchase of a volatile stock. The investor believes there is a 50% chance the stock price will rise over the next year and a 50% chance it will fall. Additionally, if the stock price decreases, there is a 20% chance it could drop by more than 15%. To assess the likelihood of making a profit, the investor could use a Monte Carlo simulation.
The process involves generating random numbers to simulate potential price movements. If a random number is less than 0.5, the stock price is assumed to fall. If it’s 0.5 or greater, the price rises. For downward scenarios, a second random number determines whether the drop exceeds 15%. By repeating this simulation 1,000 times, the investor can estimate the probability of making a profit and decide whether to proceed with the investment.
Monte Carlo simulations can also help investors diversify their portfolios. By modeling different asset mixes under various market conditions, the simulation might reveal that a combination of stocks, bonds, and real estate offers more stable returns and reduced overall risk. This enables investors to make informed decisions about asset allocation and risk management.
An ideal example of using a Monte Carlo simulation for retirement planning would involve factors like initial capital, expected withdrawal rates, investment returns, and volatility, as well as backtesting using historical data. Below is a revised example that incorporates these elements:
Example of the use of Monte Carlo Simulations to your retirement planning
Monte Carlo simulations are a powerful tool in retirement planning, allowing you to assess whether your savings can sustain you throughout retirement. Let’s consider an example where you allocate your portfolio with 50% in VT (Vanguard Total World Stock ETF) and 50% in GOVT (iShares U.S. Treasury Bond ETF). You want to simulate how your retirement savings will perform over a period of 10 years, with an initial value of $1,000,000.
You plan to withdraw $80,000 annually to cover living expenses. A Monte Carlo simulation is run to evaluate the potential outcomes of this strategy, comparing it to a benchmark portfolio (SPY, representing the S&P 500). The simulation adjusts the annual returns based on historical data and volatility, simulating thousands of potential outcomes. Here’s what the analysis reveals:
Key Outcomes
- Base Case Scenario (Average Final Value): The average final value of "My Strategy" (50% VT / 50% GOVT) is $892,788, significantly lower than SPY's average final value of $2,792,865. This indicates that while "My Strategy" offers a more conservative approach, SPY has a much higher potential for growth over the 10-year period.
- Worst Case Scenario (5th Percentile Final Value): In the worst-case scenario, "My Strategy" ends up with $245,579, while SPY results in $448,515. Although both strategies could potentially lose value in extreme conditions, SPY still offers a higher floor.
- Best Case Scenario (95th Percentile Final Value): In the best-case scenario, "My Strategy" reaches $1,716,898, whereas SPY can soar to $6,990,998. This demonstrates SPY’s greater volatility and potential for high returns.
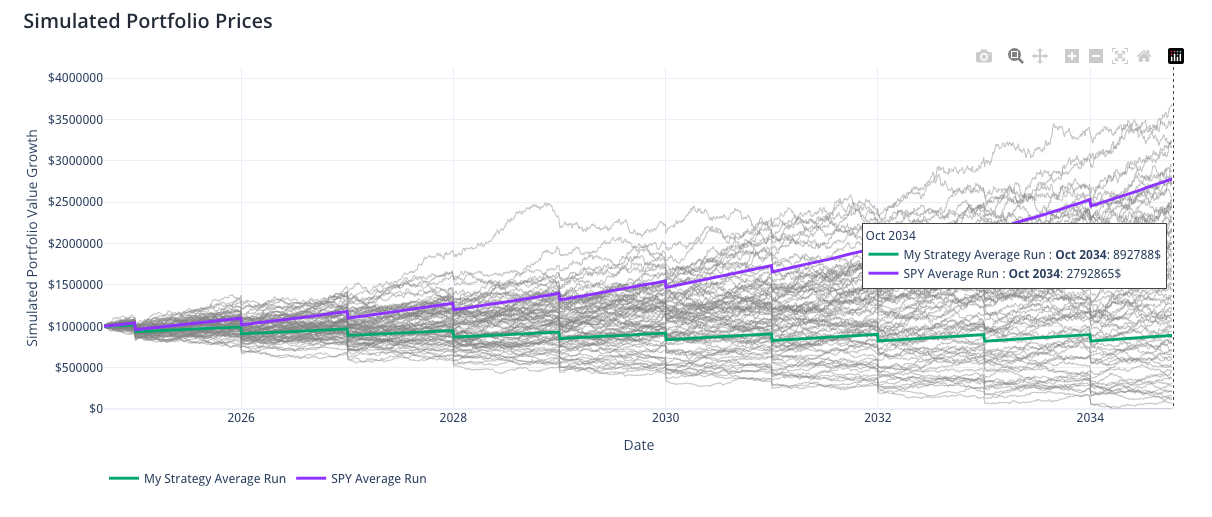
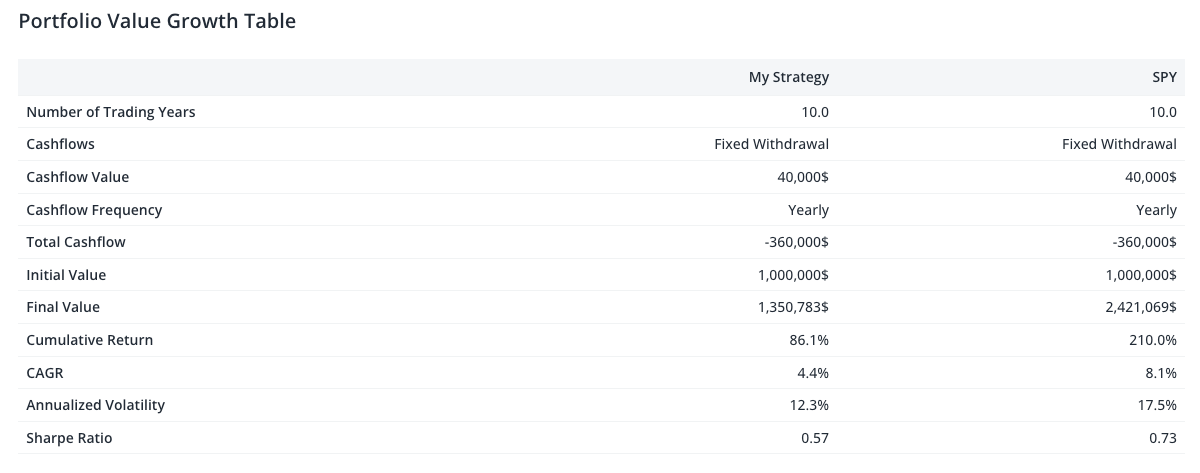
The Monte Carlo simulation over 10 years with $80,000 annual withdrawals shows that "My Strategy" is more conservative but significantly underperforms in average final value compared to SPY ($892,788 vs. $2,792,865). While "My Strategy" offers better stability in the Worst Case, SPY has far greater upside potential in the Best Case Scenario.
Understand the Limitations and Criticisms of Monte Carlo Simulations
While Monte Carlo simulations are useful, they are not without limitations. One of the main criticisms is that they assume perfectly efficient markets, where all available information is already reflected in asset prices. This assumption can be problematic, as real markets are often influenced by factors like macroeconomic trends, company leadership, market sentiment, and cyclical changes—none of which are captured by historical price data alone.
Furthermore, the simulation's reliance on historical data means that it cannot account for unprecedented events or market shifts, which could lead to outcomes that differ significantly from the simulation’s predictions. In other words, while Monte Carlo simulations provide valuable insights into potential outcomes, they do not guarantee that the most expected outcome will occur, nor do they prevent actual market movements from exceeding the simulation's wildest projections.
Conclusion: Use Monte Carlo Simulations Wisely for Financial Success
Monte Carlo simulations offer a way to model the potential outcomes of uncertain scenarios. They are particularly useful for investors, providing a detailed analysis of the risks and rewards associated with different strategies. However, it's important to remember that these simulations are not foolproof. They are based on assumptions that may not always hold true in real-world markets, and they cannot predict every possible outcome.
Despite these limitations, Monte Carlo simulations remain a valuable tool in financial analysis. By understanding their strengths and weaknesses, investors can use them to make more informed decisions, better manage risk, and ultimately achieve their financial goals.
If you're interested in applying these insights to your own financial planning, we invite you to explore our dashboard, which offers a Monte Carlo simulation feature.